Allocation of Physical Memory

메모리는 일반적으로 두 영역으로 나뉘어서 사용된다
OS 상주 영역
- interrupt vector와 함께 낮은 주소 영역 사용
사용자 프로세스 영역
- 높은 주소 영역 사용
사용자 프로세스 영역의 할당방법
Contiguous allocation
- 각각의 프로세스가 메모리의 연속적인 공간에 적재되도록 하는 방법
- Fixed partition allocattion
- Variable partition allocation
Noncontiguous allocation
- 하나의 프로세스가 메모리의 여러 영역에 분산되어 할당하는 방법
- 현대에 사용하고 있는 방식이다
- Paging : 일정한 크기로 물리 메모리 공간을 잘개 쪼갬
- Segmentation : 논리적 단위로 물리 메모리 공간을 나눔
- Paged Segmentation : 논리적 단위로 물리 메모리 공간을 나누고 Paging기법을 적용함
Contiguous Allocation
Fixed Partition Allocation (고정 분할 방식)
- 물리적 메모리를 몇개의 고정적 Partition으로 나눈다.
- 분할의 크기가 모두 동일한 방식과 서로 다른 방식이 존재한다.
- 분할당 하나의 프로그램을 적재한다. -> Paging 기법과의 차이점이다.
- 융퉁성이 없는 방식이다.
- 동시에 메모리에 load 될 수 있는 프로그램 수가 고정된다.
- 수행 가능한 프로그램의 최대 크기가 미리 분할한 크기로 제한된다. (Dynamic Loading을 잘 쓰면 더 늘릴 수 있긴하다)
- 단편화 문제: Internal, External Fragmentation이 발생한다.
External, Internal Fragmentation 발생 Case
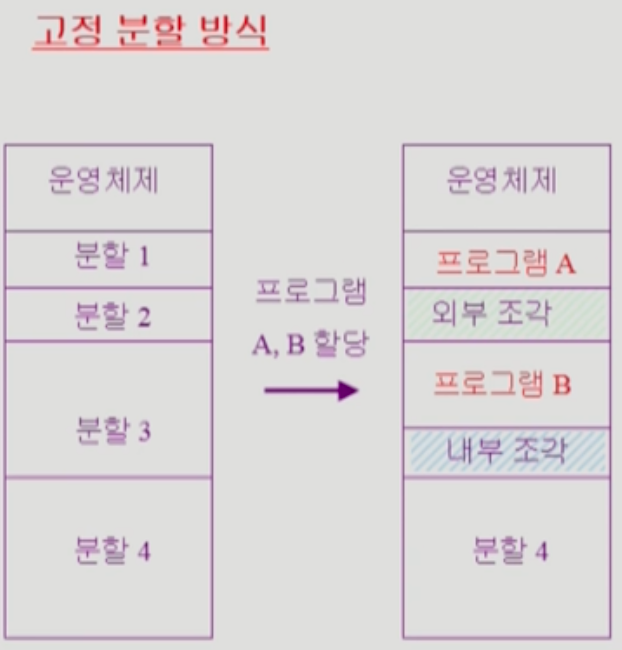
위 그림은 고정된 크기로 메모리를 분할해 놓은 Contigous Allocation 방식이다. 이때 고정된 크기는 제각각 일 수 있는데, 위의 경우에는 분할 1, 2 크기와 분할 3, 4 크기로 메모리를 분할해 놓은 형태이다.
이러한 구조에 프로그램 A와 프로그램 B를 올리게 되면 프로그램 A는 분할 1, 프로그램 B는 분할 3에 할당이 되고, 분할 3은 프로그램 B를 넣고 남은 공간이 발생하는데 이 부분이 내부 조각이 된다.
분할 2의 경우에는 해당 크기 이상의 프로그램은 넣을 수 없는 공간인 외부 조각이 된다. 이 외부조각은 해당 공간보다 작은 프로그램이 들어가게 되면 남은 공간이 다시 내부조각으로 취급될 수 있다.
Variable Partition Allocation (가변 분할 방식)
- 프로그램의 크기를 고려해서 할당한다.
- 분할의 크기, 개수가 동적으로 변한다.
- 단편화: External Fragmentation이 발생한다.
External Fragmentation 발생 Case

고정적으로 메모리를 나누지 않고 프로그램이 오는 대로 메모리에 올리는 방식이다.
위의 경우 프로그램 A, B, C가 순차적으로 올라간 상황인데, B가 종료되고 프로그램 D가 실행되는 경우에 B가 종료되고 남은 메모리 공간이 D를 올리기에는 부족하여 더 높은 주소에 올리게 되고 B가 종료되고 남은 메모리 공간은 외부조각이 된다. 또한 프로그램 D를 올리고 남은 공간 또한 외부조각이다.
Contiguous Allocation방식의 Hole 발생 문제점
결과적으로 Contiguous Allocation 방식은 Hole 을 발생시키는 할당 방식이다.
외부/내부의 단편화 문제가 발생하고 이 공간을 찾아서 프로그램을 올려야 한다. 자잘한 Hole이 계속 발생하면 메모리 낭비가 발생한다.
Hole
- 가용 메모리 공간
- 다양한 크기의 hole들이 메모리 여러곳에 흩어져 있다.
- 프로세스가 도착하면 수용 가능한 hole을 찾아서 할당한다.
- 운영체제는 a) 할당 공간 , b) 가용 공간(hole) 최신 정보를 유지해야한다.
Dynamic Storage Allocation 문제점
가변 분할 방식에서 size n인 프로그램의 요청을 만족하는 가장 적절한 hole을 찾는 문제
First - fit
- Size가 N 이상인 것 중 최초로 찾아지는 hole에 할당하는 방법
Best - fit
- Size가 N 이상인 가장 작은 Hole을 찾아서 할당하는 방법
- Hole들의 리스트가 크기순으로 정렬되지 않은 경우 최악의 경우 모든 메모리 공간을 탐색해야 한다.
- 많은 수의 아주 작은 hole들이 생성될 수 있다 .
Why? -> 들어갈 수 있는 공간 중 가장 작은 크기를 찾아서 넣기때문에 거기서 또 아주 작은 크기가 남게 된다.
Worst - fit
- 가장 큰 hole에 할당하는 방법
- 정렬되있지 않다면 모든 리스트를 탐색해야 한다.
Compaction
- External Fragmentation 문제를 해결하는 방법이다.
- 사용중인 메모리 영역을 한군데로 몰고 Hole들을 다른 한곳으로 몰아서 큰 메모리 Block으로 만드는 방법.
- 매우 비용(시간)이 많이 드는 방법이다.
- 최소한의 메모리 이동으로 Compaction하는 방법이 필요하다.
- 기본적으로 Run-Time Binding (실행 시간에 재배치 가능한 경우)에만 수행이 가능한 방법이다.
Non-Contiguous Allocation
하나의 프로세스가 불연속적인 주소공간에 분산되어서 올라갈 수 있다
- Paging
- Segmentation
- Paged Segmentation
Paging
- Virtual Memory를 일정한 사이즈의 Page단위로 나눈다.
- Physical Memory를 일정한 사이즈의 Frame단위로 나눈다. (Frame == Page, 크기)
- Virtual memory의 내용이 Physical memory에 page단위로 non-contiguous하게 저장된다.
- 일부는 backing storage, 일부는 physical memory에 저장한다.
기본 개념
- 물리적 메모리를 동일 크기의 frame 단위로 나눈다.
- 가상 메모리도 frame과 동일 크기인 Page 단위로 나눈다.
- 모든 가용 frame들을 관리한다.
- Page 테이블을 사용해서 Logical 주소를 Physical 주소로 변환한다.
- 단편화: Internal Fragmentation은 발생할 수 있다.
-> 모든 프로그램의 메모리 크기가 page의 배수로 떨어진다고 보장할 수 없으므로 마지막 부분은 page의 단위보다 작을 수 있다. 따라서 해당 부분을 메모리에 올리면 page 단위 미만의 내부조각이 발생할 수 있다.
예시 설명 (책과 책꽂이)
책과 책꽂이를 생각해보자. 이때 책을 모두 10장씩 다 쪼개서 보관해야하고 책꽂이는 모두 10장 단위로 이뤄져있다. 이때 책이 총 653장이라면 65개의 페이지와 3장이 나오게 된다. 따라서 마지막 3장을 보관하는 책꽃이는 7장의 내부 단편화 문제가 발생한다. 또한 책의 각 10장들이 어디에 위치하는지 알아야 하므로 일대일 관계의 테이블표가 필요하다. a권의 235~242장이 필요하다면 a권의 230-240장, 240-250장이 보관되어있는 책꽂이에서 가져와야할 것이다.
여기서 책의 10장 단위가 하나의 Page이고, 10장씩 저장할 수 있는 책꽂이가 Frame이다. 어느 책의 페이지가 어느 책꽂이에 위치하는지 알려주는 표가 Page Table이다.
참고사항
- Contiguous Allocation에서 논리적 주소를 물리적 주소로 변환할 때 MMU를 사용한 방식처럼 쉽게 변환하는 것이 힘들다.
- Contiguous의 방식의 경우 프로세스의 메모리가 통채로 올라가므로 물리적 주소에서 시작 주소와 한계 크기만 알면 요청하는 논리적주소에 base register를 더하기만 함으로서 물리적 주소를 구할 수 있었지만 page단위로 쪼개서 분산되어 메모리에 올라가는 Non-Contiguous Allocation 방식의 경우 단 두개의 register로 주소 변환의 구현이 불가능하다.
Page Table을 이용한 논리적 -> 물리적 주소 변환
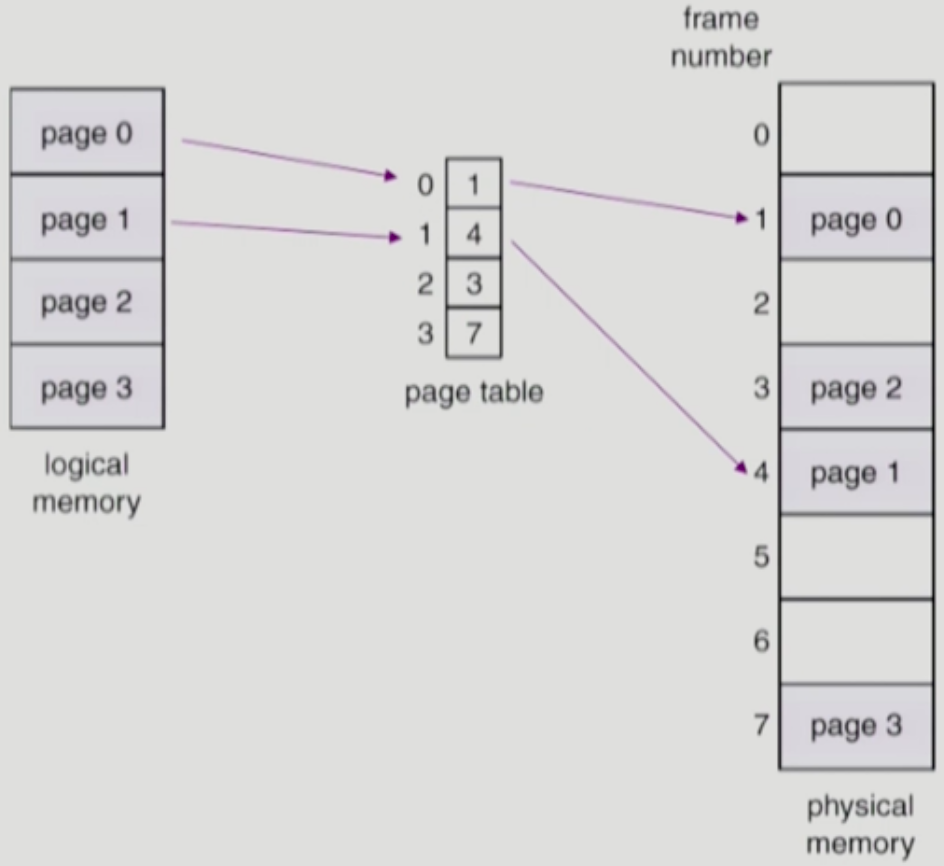
page table에 논리적 주소의 값으로 접근하고, 얻은 값으로 물리적 주소를 구하게 된다.
탐색없이 O(1)의 시간에 논리적 주소값으로 바로 Table에 접근해서 물리적 주소를 얻는것이 가능하다.
Address Translation Architecture

P
- Page Table의 원점에서 몇번 째 떨어져있는지 나타내는 Index로 Page 번호를 나타낸다.
- 책꽂이 맨앞 기준 몇 번째 인지 묻는것
D
- Page 내에서 얼마나 떨어져있는지 나타내는 offset이다.
- 이 값은 논리적 주소에서 상대적인 위치로 논리적 주소가 물리적 주소로 변환되어도 동일하게 유지된다.
- 책꽃이에 꽂혀있는 장들 중에서 몇번째 장인지 묻는것.
P값으로 page table에 해당 위치에 접근해서 물리적 주소를 얻고, 해당 물리적 주소로부터 기존 논리적 주소에 대한 offset값 d를 그대로 사용해서 접근하게된다.
즉, A책의 10장 짜리 페이지 중 하나의 페이지 내의 4번째 장은 주소변환으로 다른 곳에 위치하더라도 4번째 장은 동일한 장을 의미한다.
Page Table
Paging 방식 설명
먼저 4Kb의 Page단위로 프로그램의 메모리를 쪼개게 되고, 백만개의 Page가 나뉘어져 생성된다.
그럼 해당 Page주소와 물리적 Frame주소를 이어주는 Page 테이블 또한 100만개의 Page-Entry를 가지게 된다. 이때, Page-Entry는 4Byte이므로, Page Table은 약 400만byte ~= 4mb의 크기를 갖게된다.
이렇게 큰 크기의 메모리는 레지스터라는 작은 고속 처리장치 혹은 캐시메모리에는 들어갈 수 가 없을 뿐더러, Page Table은 각 프로그램마다 Logical Address를 Physical Address로 변환하기 위한 테이블이므로 각 프로그램마다 존재하게 된다.
따라서, Page Table은 메모리에 저장하게 된다. 그러니깐, 논리적 주소에 상응하는 물리적 메모리 주소를 알기위한 정보가 적혀있는 표인 Table이 물리적 메모리에 존재하므로, 프로그램의 논리적 주소를 통해 물리적 주소를 알기위해서
1) Page Table이 존재하는 위치에 메모리를 접근 & 2) Table로 알아낸 물리적 메모리 주소에 다시 접근해서 총 2번 접근이 필요하게 된다.
정리
- page table은 main memory에 상주한다.
- 기존 MMU에서 사용되던 Base, Limit Resgister 두개는 Paging에서 다른 용도로 사용된다.
- Page-table base register (PTBR)가 Page Table을 가리킨다.
- Page-table length register (PTLR)가 Table 크기를 갖는다.
- 모든 메모리 접근 연산에는 두 번의 Memory Access가 필요하다
- page table접근을 위해 한 번
- Page Table을 통해 얻어는 주소로 data/instruction 접근을 위해 한 번
- 속도 향상을 위해 Translation Look-aside Buffer(TLB)라 불리는 고속 lookup hadware cache를 사용한다.
- TLB은 실행하는 프로세스에 맞춰서 채워줘야 하므로, 실행하는 프로세스가 변경되면 Context Swtich가 발생하고 캐시 메모리 flush를 해서 비워줘야 한다.
Paging Hardware TLB (Cache Memory)

두번의 메모리 접근을 하는 것은 비효율적이므로 TLB라는 CPU와 메인메모리 사이에 빠르고 작은 캐시 장치를 추가하게 된다.
- TLB는 Page Table에서 자주 참조되는 일부 Page의 주소를 캐싱하고 있다.
- CPU가 논리적 주소를 주게되면 물리주소를 구하기 위해 먼저 TLB를 확인해본다.
- 있다면 바로 해당 물리적 주소로 변환하게 된다.
- 없다면 그때 Page table을 접근해서 물리적 주소를 구해서 접근하게 된다.
- TLB는 Page Table과 다르게 Table에서 바로 p번째 위치의 주소를 접근하는 방식이 아니라, 논리적 주소 값과 해당 논리 주소에 대응되는 물리적 주소값 쌍을 부분부분 갖고 있다.
따라서 원하는 논리주소를 갖고있는지 확인하기 위해서는 TLB를 처음부터 끝까지 원하는 주소값을 갖고있는지 확인해야 한다. - 이를 보안하고자 병렬처리(Parallel Search)가 가능하도록 한다.
Effective Access Time - 실제 접근 시간 계산
- TLB로 찾는데 걸리는 시간 : t
- 물리 메모리 접근 시간 : 1
- Hit Ratio (캐시적중률) = a
TLB 캐시메모리를 사용하지 않았을 경우:
1 + 1 = 2 (테이블 접근 시간 + 물리 메모리 주소 접근 시간)
TLB 캐시메모리를 사용한 경우:
(t + 1) x a + (t + 1 + 1) x (1 - a)
{ (캐시시간 + 물리 주소 접근 시간) * 성공률 } + { (캐시시간 + 테이블 접근 시간 + 물리 주소 접근 시간) * 실패율 }
= 2 + t - a
따라서 t보다 a가 크다면 더 빠른 접근을 기대할 수 있다. 보통 캐시 접근 시간은 매우 작은 값, 캐시 적중률은 1에 가까운 값을 갖는다.
Two-Level Page Table
Q. Why? 하나의 Page Table을 안쓰고 굳이 두개를 사용해서 Outer-page Table을 접근하고, 다시 Page Table을 접근해서 물리적 메모리에 접근하는 방식을 사용할까?
A. 시간상의 이득은 없다. 오히려 하나만 접근할 것을 두번 접근해야되므로 시간은 더 걸린다. 하지만, Page Table을 위한 공간이 줄어든다.
단일 Table은 논리적 주소 범위에 대해 연속적인 모든값을 table이 가져야했지만 2-Level은 유효 메모리에 대해서만 테이블을 가질 수 있다.
32-bit 운영체제에 대한 내용
32bit운영체제는 주소단위 크기가 32bit인 운영체제이다. 즉 주소를 나타내는 하나의 값의 크기는 4byte이다.
이런 구조에서 프로세스를 위한 Page Table은 각각의 Page-entry를 위한 크기를 4byte단위로 가지게 된다. 그러면 각각의 Page를 접근하기 위한 Logical Address의 Index는 32bit 상에서 나타낼수 있는 수의 범위 0 ~ 2^32 - 1이 되고,
이에 해당하는 모든 범위에 대응하는 Page table이 존재해야하므로 Page-entry x 2^32개 (1m, 100만개)의 크기를 갖게 된다. 이에 각 프로세스는 4byte * 1M = 4Mb크기의 Page Table을 갖게된다.
문제는 page table이 나타내는 논리적 주소는 대부분이 비어있는 경우가 많고, 비어있는 공간을 뛰어넘고 table을 만들 수 없다는 것이다. page table에 대한 접근은 배열과 같이 index로 접근하므로 비어있든 말든 다 만들어줘야 한다.
결과적으로 Page table은 각각의 프로세스의 논리적 주소를 물리적 주소로 변환하기 위한 테이블이므로 모든 프로그램들 마다 4mb의 크기를 갖는 table을 갖게되며, 이 모든 테이블을 메모리에 넣으면 공간적 낭비가 심할 것이다.
이러한 공간적 낭비를 해결하기 위해 나온것이 Two-Level Page Table 방법이다.
구조
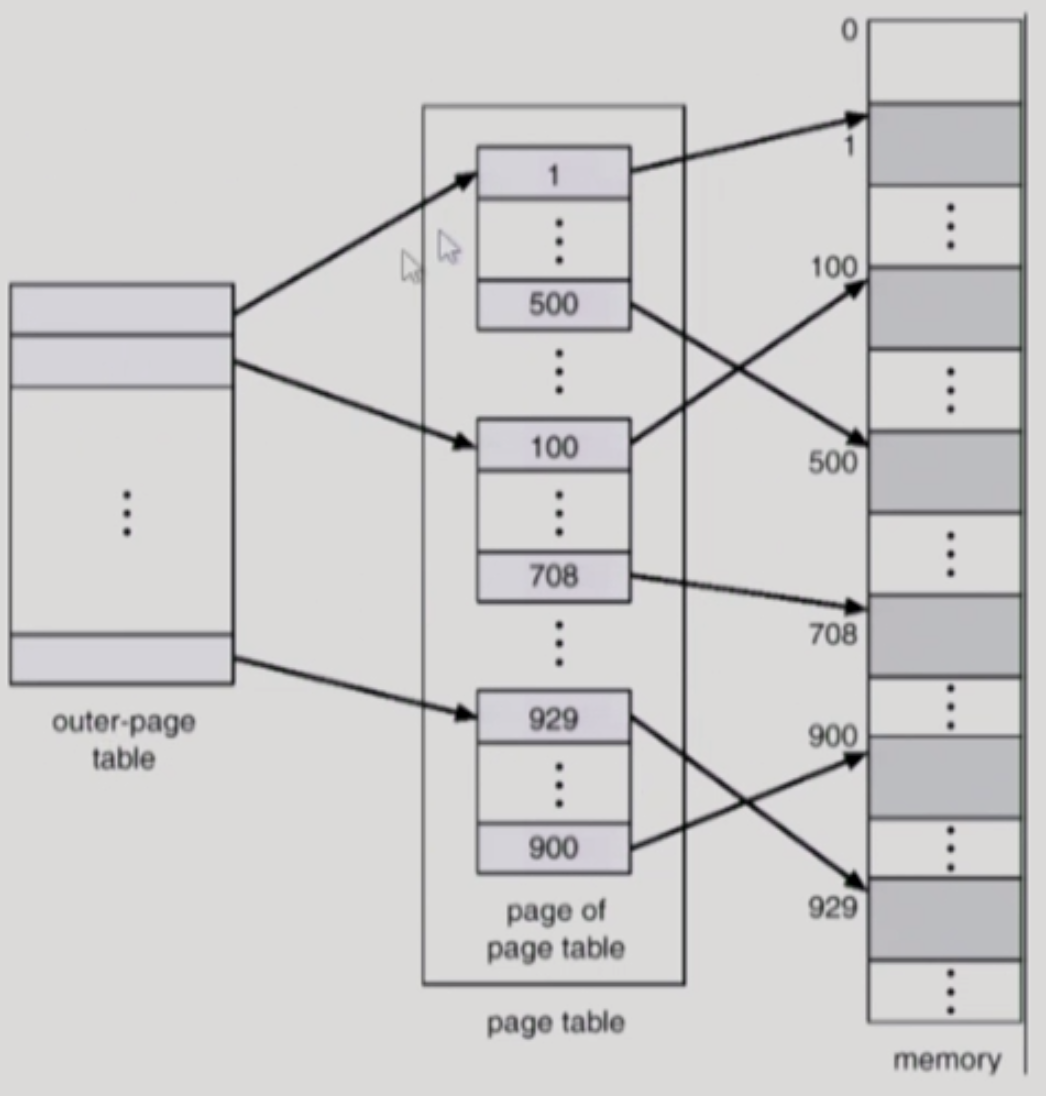
- outer 페이지 테이블의 크기 : 4kb, 길이 : 2^10
- inner 페이지 테이블 크기 : 4kb, 길이 : 2 ^ 10
- 안쪽 page table은 물리 메모리 Frame 공간 하나에 들어가있는 것으로, Page크기인 4KB와 동일하다.
따라서 page table 내에는 4Byte인 Page-Entry 1K개가 존재한다. - 이곳에 존재하는 각 page-entry들은 물리적 메모리의 Page를 가리킨다. 이후 Logical Address의 page-offset을 이용해서 page 내에서 offset으로 접근한다.
예시 설명
서울 내 모든 주소를 1-Level 페이지 테이블로 만들었다고 생각해보자. 그러면 서울 내 모든 주소들은 하나의 Page-Entry가 되어서 서울의 N번 Index로 주소에 접근하여 주소를 얻는다.
이렇게 될 경우 버려진 임야나 사용되지 않는 주소도 모두 Page-Entry로 존재하게 된다.
다시 서울 내 모든 주소를 2-Level 페이지 테이블로 만들어보자. 먼저 서울을 1024개의 구역으로 쪼갠다. 이때 필요없는 구간에 대해서는 따로 주소 테이블을 만들지 않고 NULL로 비워둔다. 이후 N번 구역으로 접근을 하여 해당 구역의 주소를 얻는다. 얻은 주소들에 대해 Offset으로 접근하여 최종적인 주소값을 얻는다.
구조
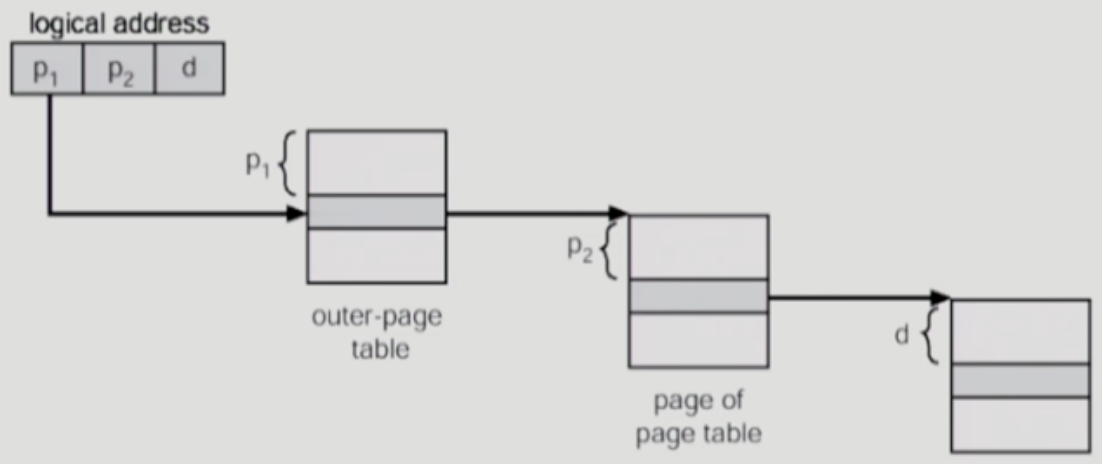
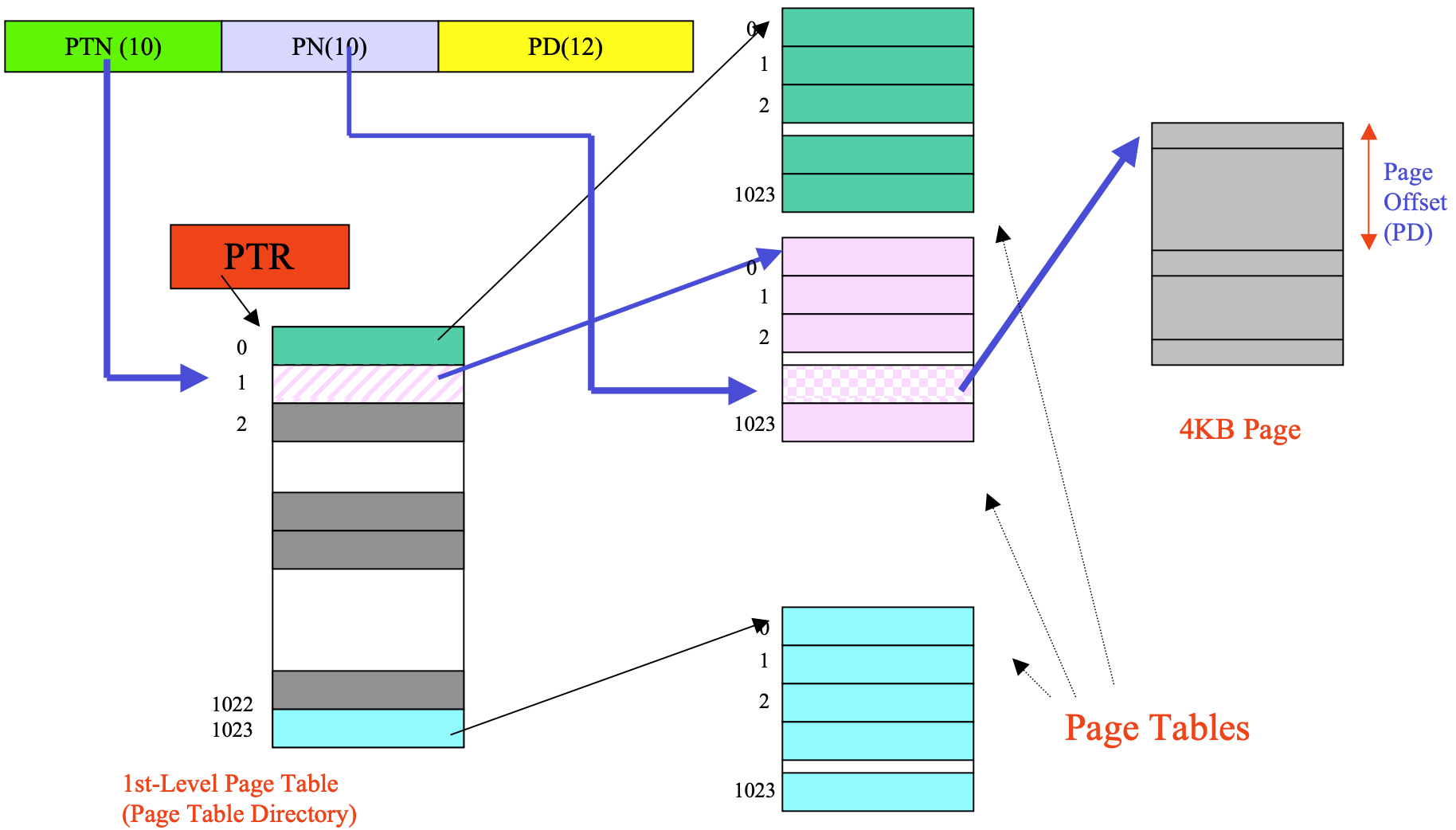
1) 논리적 주소의 값에서 P1 Page-Number를 이용해서 outer page table에 먼저 접근한다.
2) outer page table의 P1 위치의 page에서 두번째 테이블의 Page의 시작 주소를 구한다. P2의 오프셋으로 inner page table에 접근한다.
3) inner page table의 p2번째에서 얻은 값으로 물리적 메모리의 Page 물리 메모리 시작 주소를 구하고, d page offset으로 원하는 모메모리 주소에 접근한다.
Logical Address

- 32bit 운영체제의 2-Level Page Table에서 각 page-entry는 4byte, page는 4mb 이다.
- 32bit 중에서 20bit는 Page Index를 위한 공간, 10bit는 Page 내 Offset을 위한 공간이다.
Page Number (Index)
- 20bit 중에서 앞 10bit는 첫번째 Outer Page Table에서 Page를 지칭하는 Index이다.
-> 여기서 inner Page Table로 접근하기위한 Inner Page Table의 시작 주소를 알려준다. - 20bit 중에서 뒤 10bit는 두번째 Inner Page Table에서 Page를 가리키는 Index이다.
-> 앞 10bit의 인덱스로 첫번째 페이지 테이블에서 얻은 페이지 테이블의 주소에서 뒤 10bit의 Index로 접근한 페이지에서 주소를 얻는다. - 두번째 Inner Page Table에서 Index로 접근한 Page에서 얻은 물리적 메모리의 Page 주소를 통해 해당 Page로 간다.
- 마지막 12bit는 해당 Page 내 Offset으로 이용해서 특정 주소 공간에 접근한다.
나눈 기준
Page Offset, 12Bit
- 하나의 Page Size는 4Kb, 즉 4byte * 2^10 이고 byte단위로 구분하기 위해서 2^12 Byte로 보면 12bit가 필요하게 된다.
Page Number, 10Bit
- 하나의 Page는 4Kb의 크기를 가지고, Page-entry는 4byte이므로 Page는 1K(2^10)개의 page-entry를 가지게 된다. 따라서 이를 구분하기 위해서 2^10의 경우를 만들기 위한, 10bit가 필요하다.
결론
앞 10bit는 4kb 크기의 첫번째 outer page table에서 1k개의 page-entry를 구분해 접근하기 위한 변위를 위해서,
중간 10bit도 동일한 방식으로, 4kb 크기의 두번째 inner page table에서 1k개의 page-entry (4byte)를 구분해 접근 위한 변위를 위해 사용되고,
마지막 12bit는 최종적으로 얻은 주소로 접근한 물리적 메모리 공간 Page 내 Offset으로 사용된다.
결론
32bit 운영체제는 2^32개의 byte주소를 가질수 있고 이는 4gb의 크기를 갖는다. 이에 가상 메모리는 4gb를 가지게 되고, 해당 논리적 주소를 물리적 주소로 변환하기 위해 Page table을 갖게되는데, Page 크기는 4Kb이므로 100만개의 Page가 생성되므로 100만개의 page-entry(4byte)가 필요하다
근데, 논리적 주소는 비어있는 경우가 대부분이라 프로세스마다 4mb의 페이지 테이블을 생성하기 싫어서 2-level-paging을 하게 되었다.
이 경우 Table을 만들 때, Outer Page Table은 1024개의 구간을 가리키게 되고 내부의 Page Table은 비어있는 공간에 대해서는 만들지 않고 정말로 사용되는 공간에 대해서만 Inner Page Table을 생성하여 공간을 아낄수 있게 된다.